Direction for questions 115 and 116: Answer the questions based on the following information.
A, S, M and D are functions of x and y, and they are defined as follows.
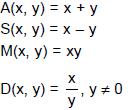
What is the value of S[M(D(A(a, b), 2), D(A(a, b), 2)), M(D(S(a, b), 2), D(S(a, b), 2))]?