Q 51 to 60 : Each of these items has a question followed by two statements. As the answer,
Mark (a), If the question can be answered with the help of statement I alone,
Mark (b), If the question can be answered with the help of statement II alone,
Mark (c), If both the statement I and statement II are needed to answer the question, and
Mark (d), If the question cannot be answered even with the help of both the statements.
What is the area under the line GHI − JKL in the given quadrilateral OPQR, knowing that all the small spaces are squares of the same area?
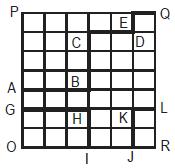
I. Length ABCDEQ is greater than or equal to 60.
II. Area OPQR is less than or equal to 1512.