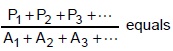Geometry
"What is the ratio of the length of PQ to that of QO?
"What is the radius of the circle II?
"The length of SO is
Let C be a circle with centre P0 and AB be a diameter of C. Suppose P1 is the mid point of the line segment P0B, P2 is the mid point of the line segment P1B and so on. Let C1, C2, C3, ... be circles with diameters P0P1, P1P2, P2P3... respectively. Suppose the circles C1, C2, C3, ... are all shaded. The ratio of the area of the unshaded portion of C to that of the original circle is
If the lengths of diagonals DF, AG and CE of the cube shown in the adjoining figure are equal to the three sides of a triangle, then the radius of the circle circumscribing that triangle will be
On a semicircle with diameter AD, chord BC is parallel to the diameter. Further, each of the chords AB and CD has length 2, while AD has length 8. What is the length of BC?
A circle with radius 2 is placed against a right angle. Another smaller circle is also placed as shown in the adjoining figure. What is the radius of the smaller circle?
In the adjoining figure, chord ED is parallel to the diameter AC of the circle. If 
, then what is the value of 
?
Two identical circles intersect so that their centers, and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is
A jogging park has two identical circular tracks touching each other, and a rectangular track enclosing the two circles. The edges of the rectangles are tangential to the circles. Two friends, A and B, start jogging simultaneously form the point where one of the circular tracks touches the smaller side of the rectangular track. A jogs along the rectangular track, while B jogs along the two circular tracks in a figure of eight. Approximately, how much faster than A does B have to run, so that they take the same time to return to their starting point?
What is the distance in cm between two parallel chords of lengths 32 cm and 24 cm in a circle of radius 20 cm?
In the X-Y plane, the area of the region bounded by the graph |x + y| + |x – y| = 4 is
In the following figure, the diameter of the circle is 3 cm. AB and MN are two diameters such that MN is perpendicular to AB. In addition, CG is perpendicular to AB such that AE:EB = 1:2, and DF is perpendicular to MN such that NL:LM = 1:2. The length of DH in cm is 
Consider the triangle ABC shown in the following figure where BC = 12 cm, DB = 9 cm, CD = 6 cm and 
What is the ratio of the perimeter of 
to that of the 
?
P, Q, S and R are points on the circumference of a circle of radius r, such that PQR is an equilateral triangle and PS is a diameter of the circle. What is the perimeter of the quadrilateral PQSR?
Mark (1) if the questions can be answered using A alone but not using B alone.
Mark (2) if the question can be answered using B alone but not using A alone.
Mark (3) if the question can be answered using A and B together, but not using either A or B alone.
Mark (4) if the question cannot be answered even using A and B together.
Rahim plans to draw a square JKLM with point O on the side JK but is not successful. Why is Rahim unable to draw the square?
A: The length of OM is twice that of OL.
B: The length of OM is 4 cm.
Two circles with centres P and Q cut each other at two distinct points A and B. The circles have the same radii and neither P nor Q falls within the intersection of the circles. What is the smallest range that includes all possible values of the angle AQP in degrees?
In a triangle ABC, the lengths of the sides AB and AC equal 17.5 cm and 9 cm respectively. Let D be a point on the line segment BC such that AD is perpendicular to BC. If AD = 3 cm, then what is the radius (in cm) of the circle circumscribing the triangle ABC?
Consider obtuse-angled triangles with sides 8 cm, 15 cm and x cm. If x is an integer then how many such triangles exist?
Consider a square ABCD with midpoints E, F, G, H of AB, BC, CD and DA respectively. Let L denote the line passing through F and H. Consider points P and Q, on L and inside ABCD such that the angles APD and BQC both equal 120°. What is the ratio of the area of ABQCDP to the remaining area inside ABCD?
Two circles, both of radii 1 cm, intersect such that the circumference of each one passes through the centre of the other. What is the area (in sq. cm.) of the intersecting region?
Let the consecutive vertices of a square S be A, B, C & D. Let E, F & G be the mid-points of the sides AB, BC & AD respectively of the square. Then the ratio of the area of the quadrilateral EFDG to that of the square S is nearest to
A one rupee coin is placed on a table. The maximum number of similar one rupee coins which can be placed on the table, around it, with each one of them touching it and only two others is
A man starting at a point walks one km east, then two km north, then one km east, then one km north, then one km east and then one km north to arrive at the destination. What is the shortest distance from the starting point to the destination?
The line AB is 6 metres in length and is tangent to the inner one of the two concentric circles at point C. It is known that the radii of the two circles are integers. The radius of the outer circle is
Q78 and 79, use the following information: ABC forms an equilateral triangle in which B is 2 km from A. A person starts walking from B in a direction parallel to AC and stops when he reaches a point D directly east of C. He, then, reverses direction and walks till he reaches a point E directly south of C.
Then D is
km north of Akm east and 1 km south of Akm west and 3 km north of A
Q78 and 79, use the following information: ABC forms an equilateral triangle in which B is 2 km from A. A person starts walking from B in a direction parallel to AC and stops when he reaches a point D directly east of C. He, then, reverses direction and walks till he reaches a point E directly south of C.
The total distance walked by the person is
Q81 85 : Data is provided followed by two statements I and II both resulting in a value, say I and II. As your answer,
Mark (a) if I > II.
Mark (b) if I < II.
Mark (c) if I = II.
Mark (d) if nothing can be said.
In ΔACD, AD = AC and ∠C = 2∠E. The distance between parallel lines AB and CD is h. Then
I. Area of parallelogram ABCD
II. Area of ΔADE
Q81 85 : Data is provided followed by two statements I and II both resulting in a value, say I and II. As your answer,
Mark (a) if I > II.
Mark (b) if I < II.
Mark (c) if I = II.
Mark (d) if nothing can be said.
k1, k2, k3 are parallel lines. AD = 2 cm, BE = 8 cm and CF = 32 cm.
Direction for questions 51 to 53: Answer these questions independently.
ABCD is a square of area 4, which is divided into four non-over lapping triangles as shown in figure. Then
the sum of the perimeters of the triangles is
Direction for questions 58 to 87: Answer the questions independently.
Which one of the following cannot be the ratio of angles in a right-angled triangle?
Direction for questions 58 to 87: Answer the questions independently.
AB ⊥ BC, BD ⊥ AC and CE bisects ∠C, ∠A = 30°. Then what is ∠CED?
Direction for questions 58 to 87: Answer the questions independently.
PQRS is a square. SR is a tangent (at point S) to the circle with centre O and TR = OS. Then the ratio
of area of the circle to the area of the square is
Direction for questions 58 to 87: Answer the questions independently.
In the adjoining figure, AC+ AB = 5AD and AC AD = 8. Then the area of the rectangle ABCD is
Direction for questions 58 to 87: Answer the questions independently.
In the given figure, AB is diameter of the circle and points C and D are on the circumference such that
∠CAD = 30° and ∠CBA = 70°. What is the measure of ∠ACD?
Direction for questions 58 to 87: Answer the questions independently.
The length of a ladder is exactly equal to the height of the wall it is learning against. If lower end of the
ladder is kept on a stool of height 3 m and the stool is kept 9 m away from the wall, the upper end of the
ladder coincides with the top of the wall. Then the height of the wall is
If ABCD is a square and BCE is an equilateral triangle, what is the measure of ∠DEC?
The figure shows a circle of diameter AB and radius 6.5 cm. If chord CA is 5 cm long, find the area
of ΔABC.
In ΔABC, ∠B is a right angle, AC = 6 cm, and D is the mid-point of AC. The length of BD is
A square, whose side is 2 m, has its corners cut away so as to form an octagon with all sides equal. Then the length of each side of the octagon, in meters, is
A certain city has a circular wall around it, and this wall has four gates pointing north, south, east and west. A house stands outside the city, 3 km north of the north gate, and it can just be seen from a point 9 km east of the south gate. What is the diameter of the wall that surrounds the city?
A ladder leans against a vertical wall. The top of the ladder is 8 m above the ground. When the bottom of the ladder is moved 2 m farther away from the wall, the top of the ladder rests against the foot of the wall. What is the length of the ladder?
Euclid has a triangle in mind. Its longest side has length 20 and another of its sides has length 10. Its area is 80. What is the exact length of its third side?
In DDEF shown below, points A, B and C are taken on DE, DF and EF respectively such that
EC = AC and CF = BC. If ∠D = 40° , then ∠ACB =
Based on the figure below, what is the value of x, if y = 10?
A city has two perfectly circular and concentric ring roads, the outer ring road (OR) being twice as long as the inner ring road (IR). There are also four (straight line) chord roads from E1, the east end point of OR to N2, the north end point of IR; from N1, the north end point of OR to W2, the west end point of IR; from W1, the west end point of OR, to S2, the south end point of IR; and from S1 the south end point of OR to E2, the east end point of IR. Traffic moves at a constant speed of 30π km/hr on the OR road, 20π km/hr on the IR road, and
on all the chord roads.The ratio of the sum of the lengths of all chord roads to the length of the outer ring road is
A city has two perfectly circular and concentric ring roads, the outer ring road (OR) being twice as long as the inner ring road (IR). There are also four (straight line) chord roads from E1, the east end point of OR to N2, the north end point of IR; from N1, the north end point of OR to W2, the west end point of IR; from W1, the west end point of OR, to S2, the south end point of IR; and from S1 the south end point of OR to E2, the east end point of IR. Traffic moves at a constant speed of 30π km/hr on the OR road, 20π km/hr on the IR road, and
on all the chord roads.Amit wants to reach N2 from S1. It would take him 90 minutes if he goes on minor arc S1 E1 on OR, and then on the chord road E1 N2. What is the radius of the outer ring road in kms?
A city has two perfectly circular and concentric ring roads, the outer ring road (OR) being twice as long as the inner ring road (IR). There are also four (straight line) chord roads from E1, the east end point of OR to N2, the north end point of IR; from N1, the north end point of OR to W2, the west end point of IR; from W1, the west end point of OR, to S2, the south end point of IR; and from S1 the south end point of OR to E2, the east end point of IR. Traffic moves at a constant speed of 30π km/hr on the OR road, 20π km/hr on the IR road, and
on all the chord roads.Amit wants to reach E2 from N1 using first the chord N1 W2 and then the inner ring road. What will be his travel time in minutes on the basis of information given in the above question?
There are two concentric circles such that the area of the outer circle is four times the area of the inner circle. Let A, B and C be three distinct points on the perimeter of the outer circle such that AB and AC are tangents to the inner circle. If the area of the outer circle is 12 square centimeters then the area (in square centimeters) of the triangle ABC would be
Three horses are grazing within a semi-circular field. In the diagram given below, AB is the diameter
of the semi-circular field with center at O. Horses are tied up at P, R and S such that PO and RO are
the radii of semi-circles with centers at P and R respectively, and S is the center of the circle
touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze
within the respective semi-circles and the horse tied at S can graze within the circle centred at S.
The percentage of the area of the semi-circle with diameter AB that cannot be grazed by the horses
is nearest to
A vertical tower OP stands at the center O of a square ABCD. Let h and b denote the length OP and AB respectively. Suppose ∠APB = 60° then the relationship between h and b can be expressed as
In the triangle ABC, AB = 6, BC = 8 and AC = 10. A perpendicular dropped from B, meets the side AC at D. A circle of radius BD (with center B) is drawn. If the circle cuts AB and BC at P and Q respectively, the AP : QC is equal to
In the diagram given below, ∠ABD = ∠CDB = ∠PQD = 90° . If AB : CD = 3 : 1, the ratio of CD : PQ is
In the figure below, AB is the chord of a circle with center O. AB is extended to C such that BC =
OB. The straight line CO is produced to meet the circle at D. If ∠ACD = y degrees and ∠AOD =
x degrees such that x = ky, then the value of k is
In the figure below, the rectangle at the corner measures 10 cm × 20 cm. The corner A of the
rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?
In the figure (not drawn to scale) given below, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC and QD is parallel to CP. In ΔARC, ∠ARC = 90 , and in ΔPQS , ∠PSQ = 90 . The length of QS is 6 cm. What is the ratio of AP : PD?
In the figure (not drawn to scale) given below, if AD = CD = BC and ∠BCE = 96 , how much is the
value of ∠DBC?
In the figure below (not drawn to scale), rectangle ABCD is inscribed in the circle with centre at O.
The length of side AB is greater than side BC. The ratio of the area of the circle to the area of the
rectangle ABCD is 
. The line segment DE intersects AB at E such that ∠ODC = ∠ADE.
The ratio AE : AD is
The length of the circumference of a circle equals the perimeter of a triangle of equal sides, and also the perimeter of a square. The areas covered by the circle, triangle, and square are c, t and s, respectively. Then,
Let S1 be a square of side a. Another square S2 is formed by joining the mid-points of the sides of S1.
The same process is applied to S2 to form yet another square S3, and so on. If A1, A2, A3,
be the
areas and P1, P2, P3,
be the perimeters of S1, S2, S3,
, respectively, then the ratio
In the figure given below (not drawn to scale), A, B and C are three points on a circle with centre O.
The chord BA is extended to a point T such that CT becomes a tangent to the circle at point C.
If ∠ATC = 30° and ∠ACT = 50°, then the angle ∠BOA is
Let ABCDEF be a regular hexagon. What is the ratio of the area of the Δ ACE to that of the hexagon ABCDEF?
A square is drawn by joining the midpoints of the sides of a given square. A third square is drawn inside the second square in the same way and this process is continued indefinitely. If side of the first square is 8 cm, the sum of the areas of all the squares such formed (in sq.cm.) is
