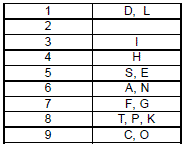
1. Looking at the code for words “is” and “as” it can be deduced that i = 3, s = 5, a = 6.
2. Now looking at the code for “Peacock”, digit 9 has only two letters according to statement 3 and 9 comes 3 times
in Peacocks code. Since 9 cannot be associated with 3 individual letters, a letter associated with 9 must occur
twice. Only “c” occurs twice. So c = 9.
3. Similarly, looking at the code for “National”, digit 6 occurs 4 times and code for i = 3. So 6 should be equal to two
letters occurring twice respectively. Those digits are “a” and “n”.
4. Between “Peacock” and “National”, letter “o” and digits “8” and “9” are common. Since, a = 8. So o = 9.
5. Between “The” and “National”, letter “t” and digit “8” are common. So t = 8, l = 1.
6. Similarly, between “The" and “Peacock", only letter "e" is common. So e = 5, h = 4.
7. In the code for “Of”, o = 9, f = 7.
8. Looking at code for “Designated”, i = 3, n = 6, a = 6, t = 8, e = 5 and between “Designated” and “Bird”, letters “I”
and “d” are common, digits “1” and “3” are common. Since i = 3, so d = 1.
9. In the code for “Designated”, g=7.
Check the following table for final codes for every letter.
For option 1, S and E have same code. So this can’t be the answer
For option 3, X, Y, Z can have same code. So this can’t be the answer.
For option 4, B can be 3 same as I. Again this is not the answer.
So only option is S, U, V. Since S and E are already associated with 5, and it can have a maximum of 3 letters.
S, U, V cannot be associated to the same number.