CBSE Class 10 Math, Polynomials

•  Zeroes of a polynomial. k is said to be zero of a polynomial p(x) if p(k) = 0

•  Graph of polynomial.

     (i)   Graph of a linear polynomial ax + b is a straight line.

     (ii)   Graph of a quadratic polynomial p(x) = ax² + bx + c is a parabola open upwards like ∪, if a > 0.

     (iii)   Graph of a quadratic polynomial p(x) = ax² + bx + c is a parabola open downwards like ∩, if a > 0.

     (iv)   In general a polynomial p(x) of degree n crosses the x-axis at atmost n points.

     

•  Relationship between the zeroes and the coefficients of a Polynomial.

     (i)   If α, β are zeroes / roots of p(x) = ax2 + bx + c, then

              

     (ii)   If α, β and γ are zeroes / roots of p(x) = ax³ + bx² + cx + d

              

     (iii)   If α, β are roots of a quadratic polynomial p(x), then p(x) = x2 – (α + β) x + αβ

              ⇒ p(x) = x² – (sum of roots) x + product of roots

     (iv)   If α, β and γ are zeroes of a cubic polynomial p(x),

              Then, p(x) = x3 – (α + β + γ) x² + (αβ + βγ + αγ) x – (αβγ)

              ⇒ p(x) = x³ – (sum of zeroes) x² + (sum of product of zeroes / roots taken two at a time)

              x – (product of zeroes)

1.  Find the zeroes of the quadratic polynomial and verify the relationship between the zeroes and coefficient of polynomial p(x) = x² + 7x + 12.

Sol. p(x) = x² + 7x + 12

              ⇒ p(x) = (x + 3)(x + 4)

              ∴ p(x) = 0 if x + 3 = 0 or x + 4 = 0

              ⇒ x = – 3 or x = – 4

              ∴– 3 and – 4 are zeros of the p(x).

              Now,

                  

2.  Find the zeroes of 4x² – 7 and verify the relationship between the zeroes and its coefficients.

Sol.  Let p(x) = 4x² – 7

                  Here coefficient of x² = 4,

                  Coefficient of x = 0 and constant term = –7.

                  

3.  Find a quadratic polynomial whose zeroes are

Sol.  Let α, β are zeroes of quadratic polynomial p(x).

                  

4.  Find a quadratic polynomial, the sum of whose zeroes is 0 and one zero is 5.

Sol.  Let zeroes are α and β.

                  ⇒α + β = Sum of zeroes

                  ⇒α + β = 0 ⇒ 5 + β = 0 ⇒β = –5

                  Now product of zeroes = αβ = 5 × (–5) = –25

                  Let polynomial p(x) = ax² + bx + c

                  

5.  Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and product of its zeroes are 5, –6 and –20 respectively.

Sol.  Let p(x) = ax³ + bx² +cx + d

                  and &alpha, &beta, γ are its zeroes.

                  ∴ α + β + γ = Sum of zeroes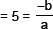

                  αβ + αγ + βγ = Sum of the products of zeroes taken two at a time

                  

                  If a = 1, then b = –5, c = –6 and d = 20

                  ∴ Polynomial, p(x) = x³ – 5x² – 6x + 20.

If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that

p(x) = q(x) × g(x) + r(x), where r(x) = 0 or degree of r(x) < degree of g(x).

Step–1. Divide the highest degree term of the dividend by the highest degree term of the divisor and obtain the remainder.

Step2. If the remainder is 0 or degree of remainder is less than divisor, then we cannot continue the division any further. If degree of remainder is equal to or more than divisor repeat step-1.

6.  Divide 4x³ + 2x² + 5x – 6 by 2x² + 3x + 1.

                  

                  ∴ Quotient is 2x – 2 and remainder is 9x – 4.

7.  Find all zeroes of polynomial

                  4x⁴ – 20x³ + 23x² + 5x – 6 if two of its zeroes are 2 and 3.

Sol. Since two zeroes are 2 and 3.

                  ∴ (x – 2)(x – 3) is a factor of given polynomial.

                  ⇒ x² – 5x + 6 is a factor of given polynomial.

                  Now

                  

                  ∴ 4x⁴ – 20x³ + 23x² + 5x – 6

                  = (x² – 5x + 6)(4x² – 1)

                  = (x – 2)(x – 3)(2x – 1)(2x + 1)

                  ∴ Zeroes of the given polynomial are